Corridietro è il nome del classico motivo a onde diffusissimo in epoca romana, soprattutto come ornato pavimentale, e molto usato anche in epoche successive. Nella sua versione più ricca, esso è costruito con due serie di spirali di Archimede che si sviluppano a specchio, scorrendo su un asse centrale. Caratteristica della spirale di Archimede è lo sviluppo con una distanza regolare, detta passo. Ne sono un esempio le grosse funi avvolte su se stesse in uscita dagli strozzascotte, che fanno bella mostra di sé sulle coperte delle barche a vela. Una spirale che, invece, si espande progressivamente, si dice logaritmica, ed è costruita sulla rotazione del rettangolo aureo. Ne è un esempio, in questo caso, la sezione della nota conchiglia detta nautilus.
La spirale di Archimede è brutta, perché l’attorcigliarsi del passo costante la rende monotona; quella logaritmica invece è molto bella perché si espande progressivamente. Essa ha però un difetto fatale, che ne impedisce l’uso ai fini della decorazione: è incommensurabile. Essendo costruita su rapporti aurei, ha misure irrazionali, quindi incompatibili con il sistema modulare, che costituisce invece l’unità di misura degli apparati decorativi. Si sa cioè da dove parte, ma non si riesce a prevedere dove arrivi, né quante volute nel frattempo sviluppi. Rimane un bel gioco matematico, ma totalmente inapplicabile dal punto di vista progettuale e costruttivo.
La spirale di Archimede, invece, avendo il passo costante, è perfettamente misurabile. In pratica essa consta di due serie di semicirconferenze concentriche, i cui fuochi sono separati e distanziati fra loro lungo una linea di riferimento, che Palladio, nel libro I, cap. XVI, dei suoi Quattro libri dell’architettura (1570), chiama cateto 〈1〉. Questa peculiarità consente di inscrivere la prima serie di queste semicirconferenze in un quadrato e, quindi, misurare e gestire il tutto con tranquillità. La serie di circonferenze contrapposta, ovviamente, si svilupperà di conseguenza una volta che la prima sarà posizionata. Per inciso, va osservato come il capolavoro progettuale della decorazione rinascimentale, rappresentato dal disegno della voluta del capitello ionico, ben illustrato nelle tavole dei trattati di Palladio, Vignola e molti altri architetti, risponda proprio all’esigenza di creare una spirale che si evolva come se fosse logaritmica, pur rimanendo perfettamente commensurabile come quella archimedea.
La spirale di Archimede si costruisce partendo da un cerchio, detto occhio, tagliato a metà dal cateto. Puntando il compasso nel punto in cui la circonferenza incontra il cateto, con apertura uguale al diametro, si traccia un arco di circonferenza inferiore. Tornando a puntare sul centro dell’occhio, con apertura tale da raccordarsi con la precedente semicirconferenza, se ne traccia uno superiore, eccetera. In pratica, quindi, il diametro dell’occhio diventa il passo della spirale. Se questa operazione viene svolta contemporaneamente, in senso opposto, su due occhi affiancati, si ottiene il corridietro: vi saranno cioè due spirali affiancate in modo da creare due spazi uguali, tali che annerendone uno si ottiene un effetto positivo-negativo.
Misurabilità, si diceva. Ora: se noi prendiamo il raggio di un occhio come modulo, il quadrato in cui il tutto viene costruito sarà di dodici moduli, che comprendono tre semicirconferenze nella parte inferiore e tre in quella superiore. Fin qui, tutto facile se non fosse che, sviluppando il pattern così ottenuto, si ottiene sì un motivo a corridietro, ma visivamente poco stimolante, nel senso che l’alternanza di positivo e negativo, seppur geometricamente corretta, non rende assolutamente l’effetto dell’onda, che invece è proprio il punto di forza del motivo stesso. La rotondità dei due occhi affiancati fa diventare il tutto perfettamente simmetrico rispetto all’asse centrale, ingenerando monotonia. Ecco quindi che gli artisti romani e rinascimentali si adoperavano per elaborare aggiustamenti e varianti su questa struttura di base canonica.
Per capire di che natura fossero questi aggiustamenti, un esempio ci è fornito dal recente ritrovamento, nel corso di scavi condotti nel centro storico di Milano, di un mosaico pavimentale romano corrispondente ad una stanza a pianta rettangolare 〈2〉. Tutto intorno ai quattro lati del rettangolo, spicca una fascia perimetrale caratterizzata da uno splendido corridietro, che colpisce per la peculiarità di avere la larghezza dell’ “onda” nera corrispondente alla metà del fondo bianco. Caratteristica, questa, oltremodo importante per un mosaico, in quando la larghezza degli elementi ornatistici è misurata a priori sulla dimensione delle tessere. Come si è riusciti ad ottenere questo rapporto 2/3 – 1/3? E come mai, nonostante ciò, l’onda nera si chiude con un bel ricciolo, dall’effetto pulsante e dinamico? Diamo di seguito la soluzione del problema, ottenuta dopo un’attenta analisi del disegno geometrico sottostante al pattern.
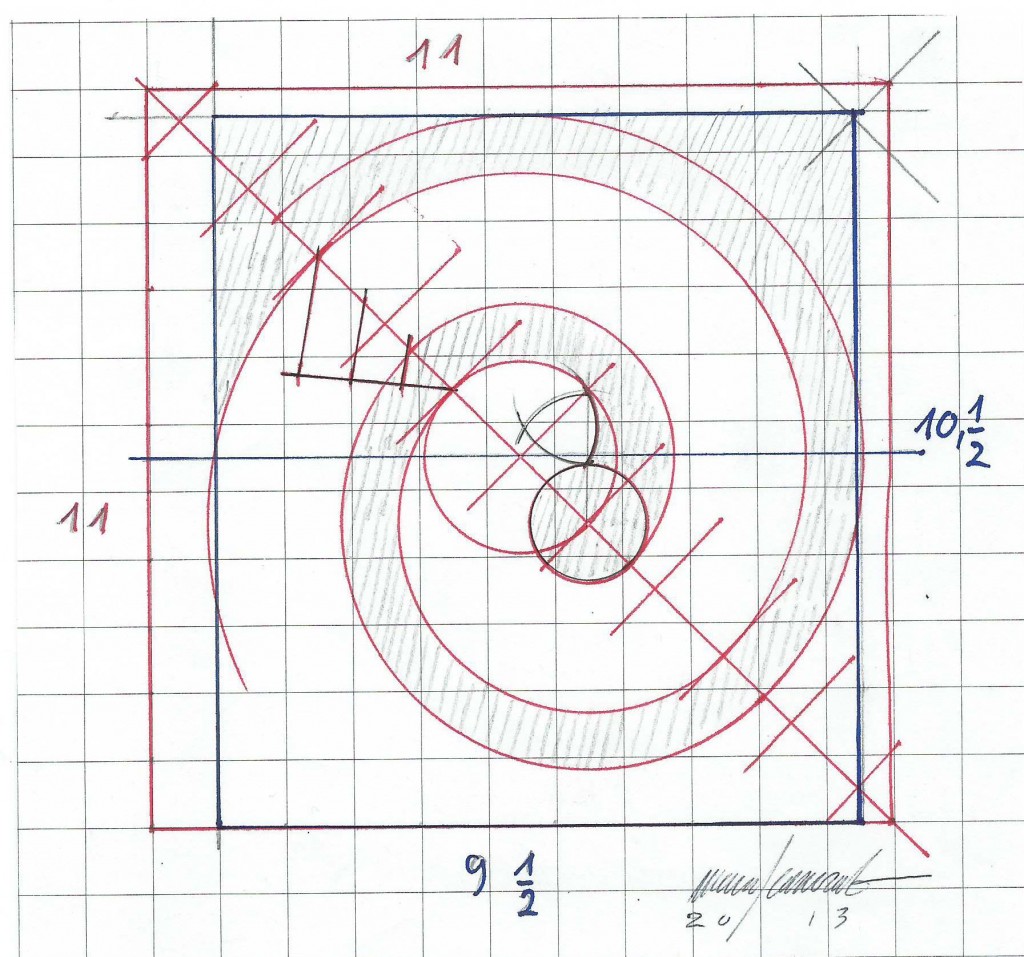
Il quadrato di partenza è di undici moduli anziché dodici, e come cateto viene usata la diagonale anziché la canonica mediana orizzontale. Le due metà dell’occhio saranno quindi determinate non dal lato del modulo, ma dalla sua diagonale. Da ciò si costruisce una singola spirale di Archimede con un passo pari al diametro dell’occhio. Si divide il passo in tre parti e sull’ampiezza della prima, vicina alla prima spirale, si costruisce la seconda spirale, che, al centro, verrà chiusa con un cerchio che avrà detta parte come raggio. Lo sviluppo delle volute costruite sulla diagonale altera un po’ i punti di congiunzione del pattern. In orizzontale, le “onde” si collegano con una ampiezza di dieci moduli. In verticale, invece, il collegamento delle varie parti bianche, a cui viene assegnato un modulo (cioè, di fatto, una tessera del mosaico), si trova ad avere solo mezzo modulo di spessore, per cui si rende necessario aggiungere un altro mezzo modulo. Le misure finali del pattern corrisponderanno perciò a dieci moduli di larghezza e ad undici e mezzo di altezza.
〈1〉 Vedi A. Palladio, I quattro libri dell'architettura, Roma, Edizioni Studio Tesi/Edizioni Mediterranee, 2008, pp. 44-52. Vedi inoltre su questa stessa rivista, per il passo palladiano in cui si spiega la costruzione della curva spiraliforme: A. Palladio-J. Vignola, Come si costruisce la voluta ionica, mar-apr 2013. 〈2〉 Il mosaico, poi distaccato e sottoposto a restauro a cura della Soprintendenza per i Beni Archeologici della Lombardia, che ringraziamo per averci consentito la riproduzione dell'immagine fotografica, proviene dai recenti scavi relativi alla domus di via Illica. In alto: particolare di spirale archimedea scolpita a bassorilievo. Sotto: Mosaico pavimentale della domus di via Illica a Milano (foto © Soprintendenza Archeologica per la Lombardia).



