I. Inapplicabilità della sezione aurea
Quello della sezione aurea è un problema squisitamente matematico, che, nel suo continuo intersecare il campo delle arti, ha generato tutta una serie di miti ed equivoci. Nostra intenzione è cercare di far luce su alcuni aspetti essenziali per il suo impiego nella decorazione. La tesi che cercheremo di dimostrare è, almeno in apparenza, paradossale: la sezione aurea in quanto tale non è applicabile al campo della decorazione, nonostante il suo rapporto numerico sia realmente presente in tantissime opere. Per ricordare al lettore cosa si intenda per sezione aurea, andiamo a rileggere la classica definizione datane dal matematico greco Euclide, seguita da uno schema esemplificativo: “Si può dire che una linea retta sia stata divisa secondo la proporzione estrema e media quando l’intera linea sta alla parte maggiore così come la maggiore sta alla minore”.
In altre parole, AB sta ad BC come AC sta ad AB. Come scrive Mario Livio in un ottimo saggio divulgativo, al quale rinviamo il lettore per ogni ulteriore approfondimento, il valore esatto del rapporto aureo «corrisponde al numero 1,6180339887…, con infinite cifre decimali prive di sequenze ripetitive; un numero “interminabile” che ha incuriosito gli uomini fin dall’antichità». E più avanti: «Il fatto che la sezione aurea non si possa esprimere per mezzo di una frazione (cioè come un “numero razionale”) significa semplicemente che è impossibile trovare due numeri interi il cui rapporto corrisponda esattamente al rapporto delle lunghezze di AB e BC […]. Dal punto di vista geometrico, trovare due numeri del genere significherebbe trovare un segmento che, poniamo, sia contenuto esattamente trentun volte in AB e diciannove volte in BC. Ma per quanto cercassimo, un segmento con questa proprietà non potremmo trovarlo. Quando, come in questo caso, due lunghezze non sono multipli interi di un’unità di misura comune, sono dette “incommensurabili”. La scoperta che il rapporto aureo è un numero irrazionale fu quindi, nel contempo, la scoperta dell’incommensurabilità» 〈1〉.
Prerogativa del rapporto aureo è, in definitiva, quella di governare una progressione costante di grandezze, senza però ammettere alcun denominatore comune fra l’una e l’altra. L’ipnotica progressione che genera rettangoli armonici e spirali complesse (dove l’intera linea diventa la parte maggiore di una linea successiva e così via all’infinito) è all’origine del fascino della sezione aurea, e spiega come mai tanti studiosi abbiano cercato le prove di una sua applicazione nelle più disparate opere d’arte, dalle piramidi egizie al Partenone. Su questo specifico punto facciamo nostra la tesi del già citato Mario Livio. Secondo Livio – che compie l’esperimento addirittura sul suo televisore 〈2〉 – si potrebbe rintracciare un rapporto aureo, se solo lo si volesse, pressoché in qualunque manufatto. Ma ciò non significa affatto che il progettista abbia coscientemente applicato la sezione aurea, tanto più che, se si parla di architetture antiche, è tutto da dimostrare che i punti scelti per le misurazioni siano corretti e non, invece, individuati ad hoc per far tornare i conti.
L’uso conscio e pertinente della sezione aurea si fa strada solo con l’opera di pochi artisti rinascimentali (in primis Piero della Francesca) che avevano anche profonde cognizioni matematiche, ma che, in quanto pittori, esulano dal nostro campo di ricerca. Noi ci occupiamo di decorazione e quindi di architettura, giacché i due termini, fino a cento anni fa, erano sinonimi. Per inquadrare il problema dal nostro punto di vista è necessario partire da quello che si potrebbe definire il “dato naturale ineludibile”. Nei cantieri antichi, infatti, le maestranze non disponevano di misuratori, livelle laser, computer o calcolatrici elettroniche, ma solo di spaghi, stecche di legno e pesi di piombo. Strumenti, questi, che non riportavano alcuna scala di misurazione incisa (il metro venne introdotto solo all’inizio dell’800 come unità di misura internazionale). Mentre, per altro verso, le unità di misura in uso (palmo, piede, cubito eccetera) presentavano ampi margini di oscillazione tra città e città.
In questa situazione, gli unici calcoli possibili in cantiere – dalla moltiplicazione dell’unità alla sua suddivisione in parti definite – venivano effettuati con numeri razionali. Più precisamente, i soli calcoli alla portata delle maestranze erano quelli eseguibili a mente, in maniera intuitiva, e cioè: il doppio, il triplo, il quadruplo… oppure la metà, un terzo, un quarto… Nessuno sarebbe stato in grado di eseguire operazioni con numeri irrazionali completi di virgole e decimali e, cosa più importante, la strumentazione disponibile ne avrebbe comunque impedito l’applicazione ai processi produttivi. Anche ammesso che l’architetto fosse stato in grado di eseguire calcoli di tale complessità, gli sarebbe poi risultato praticamente impossibile trasferirli nella prassi cantieristica. Tra lo spago del capomastro e il compasso dell’architetto – usato come strumento di misura e di calcolo, così come avviene ancor oggi nella nautica – vi era totale reciprocità.

Tutto il processo era quindi sottoposto alla legge della commensurabilità: ad ogni cosa doveva corrisponderne un’altra. Ciò implicava, in fase progettuale, l’adozione di un sottomultiplo comune, ossia di un’unità di misura astratta, il modulo (ad esempio, il diametro o il raggio della colonna negli ordini architettonici), la quale veniva poi traslitterata in cantiere nell’unità di misura locale 〈3〉.
Parola-chiave di tutto il processo era “simmetria” (in latino symmetria, in greco συμμετρία) il cui etimo di derivazione greca, un composto di syn (“con”, “insieme”) e mètron (“misura”), significa “avente la stessa misura”. Per noi, moderni fruitori del sistema metrico decimale, si tratta di un’idea obsoleta, tant’è che nel linguaggio corrente il concetto di simmetria si usa pressoché esclusivamente in accezione matematico-geometrica, assiale. Ma nelle epoche in cui le unità di misura erano varie e molteplici, basilare per il funzionamento di qualunque cantiere era appunto la legge della syn-metría, i cui requisiti di chiarezza e computabilità si collocavano evidentemente all’opposto rispetto a quelli della sezione aurea.
Nello specifico della decorazione, poi, alla simmetria si affiancava un’altra legge fondamentale: l’isometria, cioè la costanza degli angoli nella successione di figure geometriche di base impiegate nella copertura della superficie. Griglie, intrecci, tassellature, connessioni di pattern sono infatti possibili solo in condizioni di isometria.
Ora: la sezione aurea, proprio in quanto numero irrazionale indicante un rapporto fra grandezze incommensurabili fra loro perché prive di un sottomultiplo comune, è inapplicabile alla decorazione architettonica perché antitetica ai principi di simmetria e isometria necessari a governare tutto il processo che, dall’ideazione e progettazione, porta poi all’esecuzione e alla posa dei manufatti. Questo, almeno fino all’entrata in vigore, poco più di cento anni fa, del sistema metrico decimale, sistema che con la proprie scale progressive consente il trasferimento e l’applicazione anche di misure derivanti da calcoli con numeri irrazionali.
II. Uso del rapporto aureo
Se simmetria ed isometria sono le leggi fondamentali, ineludibili, che hanno governato l’architettura e la decorazione storiche fino agli inizi del secolo XX, allora si capisce perché alla base dei loro linguaggi espressivi vi siano sempre stati il quadrato e il triangolo equilatero: figure isometriche per antonomasia, col cerchio a fare da elemento normativo e di controllo. Tuttavia, osservando le opere realizzate, si scopre che la quasi totalità degli spazi e delle superfici sono rettangolari. Lo sono le piante degli edifici, le porte, le finestre, le pareti in muratura, i mobili. Il rettangolo è una figura geometrica che ha sì quattro angoli uguali, ma i suoi lati lo sono a coppie, e questa uguaglianza tra coppie vale per qualsiasi rapporto esista fra le stesse. Insomma, il rettangolo è una figura arbitraria, ostile al governo delle succitate leggi della simmetria e dell’isometria.
Questo è il punto chiave: qualora si debba sviluppare una superficie rettangolare (pianta di edificio, parete in muratura, ecc.), come la si potrà rendere compatibile con le ferree leggi della composizione? L’ipotesi di un rettangolo costruito con grandezze scelte a caso è da scartare a priori: l’architetto deve dare precise indicazioni su come si tracci la figura sul terreno, e non può certo lasciare che le maestranze procedano a loro piacimento. A sua volta, mai e poi mai il decoratore potrebbe inserire una figura arbitraria nella propria griglia, altrimenti l’intera progressione dei pattern si scompaginerebbe.
Questo per quanto attiene al punto di vista operativo, ma anche il fattore estetico pesa, e non poco. Quale rettangolo conviene disegnare? Meglio lungo o corto? Se si tenta di risolvere la questione ricorrendo al modulo quadrato, sorgono immediatamente delle difficoltà. Due quadrati compongono infatti un rettangolo dalle ottime caratteristiche isometriche, ma troppo lungo. Il rettangolo ottenuto da un quadrato e mezzo è invece troppo corto, e se si tenta di fissare dimensioni intermedie usando i quarti di quadrato, si espone la griglia ad una frammentazione poi difficilmente gestibile dal punto di vista compositivo.
Da parte sua, l’architetto può risolvere il dimensionamento del rettangolo affiancando l’uno all’altro moduli quadrati, ma col rischio di comporre una figura troppo monolitica e rigida. Nel caso in cui, ad esempio, egli dovesse progettare la pianta di una cattedrale, un solo rettangolo, anche se ben dimensionato, risulterebbe completamente inadeguato per contemperare la disposizione dei pilastri, lo spessore delle mura, l’innesto del transetto, la chiusura absidata, e numerosi altri aspetti. Occorrerà predisporre un sistema dinamico che consenta di tracciare una griglia generale all’interno della quale operare le scelte compositive, le quali dovranno a loro volta essere tracciabili sul terreno con lo spago e l’aratro trainato dai buoi.
Il decoratore, a sua volta, ha di fronte spazi interni da ricoprire con tarsie governate da rigide leggi isometriche, all’interno delle quali non gli è consentito inserire rettangoli eccedenti o anomali rispetto alla griglia generale adottata. La soluzione dovrà quindi essere tutta interna al quadrato, in quanto figura isometrica di base, e portare alla creazione di una griglia normativa.
Tra le esperienze più rilevanti condotte dal pioniere della psicologia sperimentale Gustav Theodor Fechner (1801-77), sono da ricordare quelle, effettuate attraverso ripetuti sondaggi, riguardanti la percezione delle forme rettangolari. Esse accertarono come il picco delle preferenze in termini di gradevolezza estetica andasse ai rettangoli aurei o, comunque, molto vicini al rapporto aureo 〈4〉. Tale orientamento da parte dei fruitori non si spiega certo col rapporto numerico, in sé e per sé impossibile da computare ad occhio nudo, ma piuttosto con la dimensione ottimale, “empatica”, della figura: né troppo lunga (come accade col rettangolo composto di due quadrati), né troppo corta (un quadrato e mezzo).
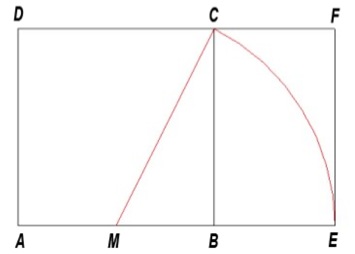
Ora, come si costruisce un rettangolo aureo? Tracciato un quadrato, lo si divide in due rettangoli tracciando la mediana verticale, per ribaltare poi verso l’esterno la diagonale del secondo rettangolo. Si otterrà così un rettangolo le cui coppie di lati stanno tra loro in rapporto aureo. Ma non basta. Se si traccia una nuova linea congiungente il punto mediano inferiore del quadrato di partenza col vertice superiore del rettangolo aureo e la si ribalta verso l’esterno, ecco apparire un altro rettangolo, un po’ più allungato del precedente. L’operazione potrà essere ripetuta più e più volte, finché la progressione non sarà, di fatto, pressoché irrilevante. Questo processo si chiama “dinamizzazione del quadrato” e consente, attraverso successivi ribaltamenti di diagonali, di costruire una serie di rettangoli “razionali”, tracciabili a terra con lo spago.
Pertanto, l’architetto che ponesse un rombo al centro del suo progetto e ne dinamizzasse le diagonali nelle quattro direzioni, otterrebbe una griglia di punti (riportabile con lo spago in cantiere) sulla quale operare le proprie scelte compositive. Ovvio che all’interno della griglia vi saranno rapporti aurei e grandezze esprimibili con numeri irrazionali, ma né all’architetto né alle maestranze sarà stato richiesto un solo calcolo numerico.
Per il decoratore, invece, la griglia generale isometrica è ineludibile, perché egli opera già all’interno di uno spazio dato, ma è altresì vero che, lavorando sulle diagonali dei poligoni regolari, perfettamente inscrivibili nella griglia, egli potrà ottenere tutta una serie di rettangoli aurei. Il caso più frequente, in particolare nell’arte islamica, è quello dei tre rettangoli aurei incrociati, determinati dalle diagonali parallele all’interno di un esagono. Un esempio da manuale è dato dall’incrocio delle diagonali del pentagono da cui si genera la stella pentagonale, i cui segmenti sono in rapporto aureo. Ancora una volta, il riconoscimento del rapporto aureo attiene alla matematica, mentre chi opera nelle vesCostruzione del rettangolo aureo a partire dal quadrato.ti di decoratore può far uso di rapporti aurei senza per questo dover eseguire alcun calcolo matematico.
In conclusione, possiamo dire che il paradosso dell’inapplicabilità della sezione aurea in architettura e in decorazione – pur se nelle proporzioni interne delle opere realizzate vi è una costante presenza di rapporti aurei – sia più apparente che reale, nel senso che una spiegazione c’è, e molto semplice. Tale spiegazione risiede nell’utilizzo intuitivo che da sempre è stato fatto delle diagonali delle figure geometriche regolari: nel loro dispiegarsi, tali diagonali danno effettivamente luogo ai rapporti aurei, anche se poi tali rapporti, nella loro fattispecie matematica, restano sconosciuti ai più. Pertanto, la giusta via per interpretare la presenza della sezione aurea nei manufatti architettonici e decorativi, e per ripercorrerne concretamente la gestazione, non sarà quella, tortuosa e ridondante, dell’analisi matematica, ma quella, breve ed intuitiva, della progressione geometrica.
〈1〉 M. Livio, La sezione aurea. Storia di un numero e di un mistero che dura da tremila anni, Milano, Rizzoli, 2003, pp. 13-15. 〈2〉 M. Livio, La sezione aurea, cit., pp. 74-75. 〈3〉 Per il lettore interessato al tema delle misurazioni, la fonte canonica resta A. Palladio, I quattro libri dell'architettura, Pordenone, Edizioni Studio Tesi, 2008 (ed. or. 1570), e in particolare il libro I. 〈4〉 Cfr. M. Livio, La sezione aurea, cit., pp. 263-265. In alto: compasso per la misurazione del rapporto aureo nella versione realizzata nel 1954 per il Premio ADI - Compasso d'Oro. Sotto: forma stellare inscritta in un pentagono.




